Đề bài
Cho hình vẽ sau:
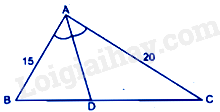
Tỉ số diện tích tam giác ABD và tam giác ADC là:
-
A.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{5}{6}\)
-
B.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{4}{5}\)
-
C.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{2}{3}\)
-
D.
\(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{3}{4}\)
Phương pháp giải
Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Vì hai tam giác ADC và ADB có cùng đường cao xuất phát từ đỉnh A xuống BC.
Do đó, \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{{BD}}{{DC}}\)
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{15}}{{20}} = \frac{3}{4}\)
Vậy \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{3}{4}\)
Đáp án : D