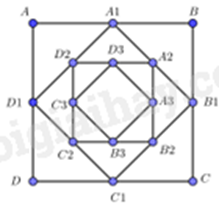
Cho hình vuông ABCD có cạnh bằng 4cm. Người ta dựng hình — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về tổng cấp số nhân lùi vô hạn: Cấp số nhân lùi vô hạn $\left( {{u_n}} \right)$ với công bội q, số hạng đầu ${u_1}$ thì có tổng là $S = \frac{{{u_1}}}{{1 - q}}$

Ta có: ${S_1} = {S_{ABCD}} = {4^2};{S_2} = {S_{{A_1}{B_1}{C_1}{D_1}}} = {\left( {\frac{{4\sqrt 2 }}{2}} \right)^2} = \frac{{{4^2}}}{2};{S_3} = {S_{{A_2}{B_2}{C_2}{D_2}}} = {\left( {\frac{{4\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{{{4^2}}}{{{2^2}}}$;…

${S_n} = {S_{{A_n}{B_n}{C_n}{D_n}}} = {4^2}.\frac{1}{{{2^{n - 1}}}}$;…

Như vậy, các số ${S_1};{S_2};...;{S_n};...$ lập thành một cấp số nhân lùi vô hạn có ${S_1} = {4^2},q = \frac{1}{2}$

Do đó: $S = {S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - q}} = \frac{{{4^2}}}{{1 - \frac{1}{2}}} = {2.4^2} = 32\left( {c{m^2}} \right)$