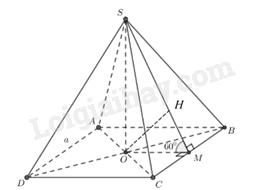
Cho khối chóp đều \(S \cdot ABCD\) có cạnh đáy là \(a\), các mặt bên tạo với đáy một góc \(60^\circ \), O là tâm đáy. Khẳng định sau đây đúng hay sai?
a) Thể tích hình chóp là: \(\frac{{{a^3}\sqrt 3 }}{2}\)
b) Độ dài cạnh bên của hình chóp là: \(\frac{{a\sqrt 5 }}{2}\)
c) Khoảng cách \(d\left( {O;\left( {SCB} \right)} \right)\) bằng: \(\frac{{a\sqrt 3 }}{4}\)
d) Khoảng cách \(d\left( {AD;SC} \right) = \frac{{a\sqrt 3 }}{3}\)
a) Thể tích hình chóp là: \(\frac{{{a^3}\sqrt 3 }}{2}\)
b) Độ dài cạnh bên của hình chóp là: \(\frac{{a\sqrt 5 }}{2}\)
c) Khoảng cách \(d\left( {O;\left( {SCB} \right)} \right)\) bằng: \(\frac{{a\sqrt 3 }}{4}\)
d) Khoảng cách \(d\left( {AD;SC} \right) = \frac{{a\sqrt 3 }}{3}\)
a) Thể tích của khối chóp có diện tích đáy \(B\), chiều cao \(h\) là \(V = \frac{1}{3}h.B\)
b) Áp dụng định lí Pytago
c) Áp dụng hệ thức lượng trong tam giác vuông
d) \(d\left( {AD;SC} \right) = 2d\left( {O;\left( {SCB} \right)} \right)\)
a) Sai.
Gọi \(M\) là trung điểm BC, Góc giữa mặt bên \((SBC)\) và mặt phẳng \((ABCD)\) là góc \(\widehat {SMO} = 60^\circ \).
Xét \(\Delta SOM\) có \(OM = \frac{a}{2},SMO = 60^\circ \) thì
\(SO = OM \cdot \tan \widehat {SMO} = \frac{a}{2} \cdot \sqrt 3 = \frac{{a\sqrt 3 }}{2}\)
Nên \({V_{S.ABCD}} = \frac{1}{3}SO{S_{AGCD}} = \frac{{{a^3}\sqrt 3 }}{6}(dvtt)\).
b) Đúng.
Đúng. Xét \(\Delta SOB\) vuông tại O ta có:
\(SB = \sqrt {O{M^2} + O{B^2}} = \sqrt {\frac{{3{a^2}}}{4} + \frac{{2{a^2}}}{4}} = \frac{{\sqrt 5 a}}{2}\).
c) Đúng.
Kẻ OH vuông góc với SM khi đó \(d\left( {O;\left( {SCB} \right)} \right) = OH\)
Xét \(\Delta SOM\)vuông tại O có: \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{{16}}{{3{a^2}}} \Rightarrow OH = \frac{{a\sqrt 3 }}{4}\)
d) Sai
Vì \(AD//CB\) mà \(CB \subset \left( {SBC} \right)\) nên
\(d\left( {AD;SC} \right) = d\left( {AD;\left( {SCB} \right)} \right) = d\left( {A;\left( {SCB} \right)} \right) = 2d\left( {O;\left( {SCB} \right)} \right) = \frac{{a\sqrt 3 }}{2}\)