Cho khối hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có đáy là hình vuông, \(BD = 2a\), góc phẳng nhị diện \(\left[ {A',BD,A} \right]\) bằng \(30^\circ \). Tính độ dài cạnh AA'
-
A.
\(\frac{{2a\sqrt 3 }}{3}\).
-
B.
\(\frac{a}{3}\).
-
C.
\(\frac{{a\sqrt 3 }}{6}\).
-
D.
\(\frac{{a\sqrt 3 }}{3}\).
Xác định góc giữa hai mặt phẳng tạo thành.
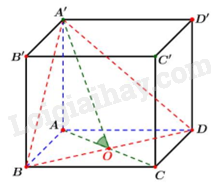
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AO}\\{BD \bot AA'}\end{array} \Rightarrow BC \bot \left( {A'AO} \right) \Rightarrow BD \bot A'O} \right.\).
Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{\left( {A'BD} \right) \cap \left( {ABD} \right) = BD}\\{A'O \bot BD}\\{AO \bot BD}\end{array}\; \Rightarrow \left[ {A',BD,A} \right] = \widehat {A'OA} = 30^\circ } \right.\).
Xét vuông tại \(A\), ta có: \({\rm{tan}}\widehat {A'OA} = \frac{{AA'}}{{AO}} \Rightarrow AA' = \frac{1}{{\sqrt 3 }} \cdot a = \frac{{a\sqrt 3 }}{3}\).
Đáp án D.
Đáp án : D