Cho khối lăng trụ ABC cdot A'B'C' có đáy ABC là tam giác — Không quảng cáo

Gọi H là trung điểm BC, M là trung điểm của B’C’

$\Rightarrow A'H \bot \left( {ABC} \right)$ và $A'MH = 30^\circ$ từ đó tìm BC, AH và tính thể tích lăng trụ.

Do $A'A = A'B = A'C = a$ nên hình chiếu của A’ xuống (ABC) là trọng tâm của $\Delta ABC$

Gọi H là trung điểm BC, M là trung điểm của B’C’

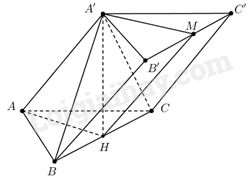
Do $\left\{ {\begin{array}{*{20}{l}}{BC \bot AH}\\{BC \bot A'H}\end{array}} \right. \Rightarrow BC \bot \left( {AA'H} \right) \Rightarrow BC \bot AA' \Rightarrow BC \bot HM$

$\begin{array}{*{20}{l}}{ \Rightarrow \left( {\left( {ABC} \right),\left( {BCC'B'} \right)} \right) = \left( {\left( {A'B'C'} \right),\left( {BCC'B'} \right)} \right) = A'MH = 30^\circ }\\{ \Rightarrow A'H = HM.\sin 30^\circ  = \frac{a}{2}}\\{ \Rightarrow A'M = \frac{{A'H}}{{\tan 30^\circ }} = \frac{{a\sqrt 3 }}{2} \Rightarrow BC = 2A'M = a\sqrt 3 }\\{ \Rightarrow V = A'H.\frac{1}{2}AH.BC = \frac{1}{2}.\frac{a}{2}.\frac{{a\sqrt 3 }}{2}.a\sqrt 3 {\rm{ \;}} = \frac{{3{a^3}}}{8}}\end{array}$

Đáp án C.