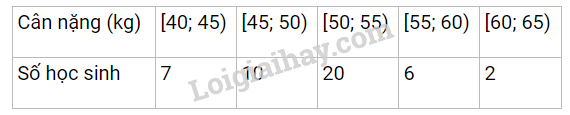
Cho mẫu số liệu về cân nặng kg của 45 học sinh lớp 11A được — Không quảng cáo

a) Tứ phân vị thứ nhất ${Q_1}$ là 47

b) Trung vị ${M_e}$ là 51,4

c) Tứ phân vị thứ ba ${Q_3}$ là 54,2

d) Mốt ${M_o} = 20$

Sử dụng công thức tính tứ phân vị của mẫu số liệu và Mốt

Cỡ mẫu là n = 7 + 10 + 20 + 6 + 2 = 45

Gọi x ₁ , x ₂ , ….., x ₄₅ là cân nặng của 45 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.

Khi đó, trung vị là x ₂₃ . Do giá trị x ₂₃ thuộc nhóm [50; 55) nên nhóm này chứa trung vị.

Do đó p = 3; a ₃ = 50, m ₃ = 20; m ₁ + m ₂ = 7 + 10 = 17; a ₄ – a ₃ = 55 – 50 = 5

Khi đó

${M_e} = {a_3} + \frac{{\frac{n}{2} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{45}}{2} - 17}}{{20}}.5 \approx 51,4$.

Vậy M _e = 51,4.

Từ M _e = 51,4, suy ra Q ₂ = 51,4.

- Tứ phân vị thứ nhất Q ₁ là trung vị của nửa dãy bên trái Q ₂ nên ${Q_1} = \frac{{{x_{11}} + {x_{12}}}}{2}$

Do x ₁₁ và x ₁₂ đều thuộc nhóm [45; 50) nên nhóm này chứa Q ₁ . Do đó, p = 2, a ₂ = 45, m ₂ = 10, m ₁ = 7; a ₃ – a ₂ = 5.

Ta có ${Q_1} = {a_2} + \frac{{\frac{n}{4} - {m_1}}}{{{m_2}}}({a_3} - {a_2}) = 45 + \frac{{\frac{{45}}{2} - 7}}{{10}}.5 \approx 47,1$

- Tứ phân vị thứ ba Q ₃ là trung vị của nửa dãy bên phải Q ₂ nên ${Q_3} = \frac{{{x_{34}} + {x_{35}}}}{2}$.

Do x ₃₄ và x ₃₅ đều thuộc nhóm [50; 55) nên nhóm này chứa Q ₃ . Do đó, p = 3, a ₃ = 50, m ₃ = 20, m ₁ + m ₂ = 7 + 10 = 17; a ₄ – a ₃ = 55 – 50 = 5.

Ta có ${Q_3} = {a_3} + \frac{{\frac{{3n}}{4} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{3.45}}{4} - 17}}{{20}}.5 \approx 54,2$ .

Vậy tứ phân vị: Q ₁ ≈ 47,1; Q ₂ ≈ 51,4; Q ₃ ≈ 54,2.

- Ta thấy tần số lớn nhất là 20 nên nhóm chứa mốt là nhóm [50; 55).

Ta có j = 3, a ₃ = 50, m ₃ = 20, m ₂ = 10, m ₄ = 6, h = 55 – 50 = 5

Khi đó

${M_0} = {a_3} + \frac{{{m_3} - {m_2}}}{{\left( {{m_3} - {m_2}} \right) + \left( {{m_3} - {m_4}} \right)}}h = 50 + \frac{{20 - 10}}{{(20 - 10) + (20 - 6)}}.5 \approx 52,1$

Vậy M _o ≈ 52,1.