Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:
-
A.
\(AC = \frac{4}{3}MC\)
-
B.
\(AC = \frac{3}{2}MC\)
-
C.
\(AC = \frac{2}{3}MC\)
-
D.
\(AC = MC\)
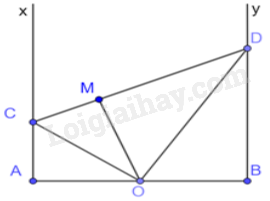
Tam giác OAC và tam giác DBO có: \(\widehat {OAC} = \widehat {DBO} = {90^0},\widehat {COA} = \widehat {BDO}\) (cùng phụ với góc DOB)
Do đó, \(\Delta OAC \backsim \Delta DBO \Rightarrow \frac{{OC}}{{OD}} = \frac{{AC}}{{OB}}\)
Mà \(OA = OB \Rightarrow \frac{{OC}}{{OD}} = \frac{{AC}}{{OA}} \Rightarrow \frac{{OC}}{{AC}} = \frac{{OD}}{{OA}}\)
Tam giác OCD và tam giác ACO có: \(\widehat {CAO} = \widehat {COD} = {90^0},\frac{{OC}}{{AC}} = \frac{{OD}}{{OA}}\)
Do đó, \(\Delta OCD \backsim \Delta ACO \Rightarrow \widehat {OCD} = \widehat {ACO}\)
Chứng minh được \(\Delta OAC = \Delta OMC\left( {ch - gn} \right) \Rightarrow AC = MC\)
Đáp án : D