Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Cho parabol (P): \(y = {x^2}\) và điểm A(-3;0). Xác định điểm M thuộc (P) sao cho khoảng cách AM là ngắn nhất. Tung độ của điểm M bằng bao nhiêu?
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Thiết lập hàm số biểu diễn bình phương độ dài AM theo biến x là hoành độ. Lập bảng biến thiên cho hàm số, tìm x để hàm số đó đạt giá trị nhỏ nhất.
Gọi \(M(x;{x^2})\) là một điểm bất kì của parabol (P).
Ta có: \(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\).
AM nhỏ nhất khi và chỉ khi \(f(x) = A{M^2}\) nhỏ nhất.
Xét \(f(x) = {x^4} + {x^2} + 6x + 9\).
Có \(f'(x) = 4{x^3} + 2x + 6 = 0 \Leftrightarrow x = - 1\).
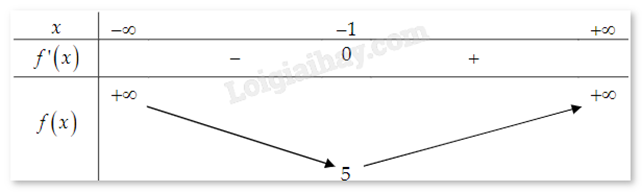
Dựa vào bảng biến thiên, ta suy ra f(x) đạt giá trị nhỏ nhất tại x = -1.
Như vậy, điểm M cần tìm có tọa độ (-1;1). Tung độ của M bằng 1.