Đề bài
Cho tam giác \({\rm{ABC}},{\rm{AC}} = 2{\rm{AB}},{\rm{AD}}\) là đường phân giác của tam giác \({\rm{ABC}}\), tính \(\frac{{BD}}{{CD}} = \) ?
-
A.
\(\frac{{BD}}{{CD}} = 1\)
-
B.
\(\frac{{BD}}{{CD}} = \frac{1}{3}\)
-
C.
\(\frac{{BD}}{{CD}} = \frac{1}{4}\)
-
D.
\(\frac{{BD}}{{CD}} = \frac{1}{2}\)
Phương pháp giải
Áp dụng tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra kết quả của đề bài.
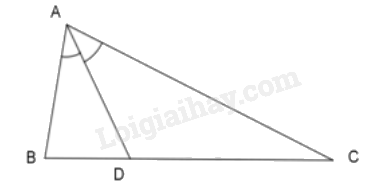
Vì \(AD\) là phân giác của \(\Delta ABC\) nên: \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\)
Theo bài, ta có: \(AC = 2AB\) suy ra \(\frac{{AB}}{{AC}} = \frac{1}{2}\) hay \(\frac{{BD}}{{DC}} = \frac{1}{2}\)
Đáp án D.
Đáp án : D