Đề bài
Cho tam giác ABC bất kì và điểm D nằm trên cạnh BC.
Khẳng định sai là:
-
A.
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
-
B.
\(\widehat {CAD} + \widehat {BAD} + \widehat {BAC} = 180^\circ \)
-
C.
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
-
D.
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Phương pháp giải
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ
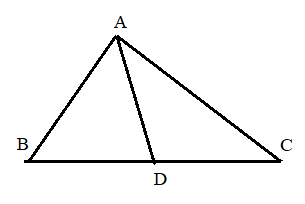
Áp dụng định lí tổng số đo 3 góc trong 3 tam giác ABD, ACD và ABC, ta được:
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Vậy A,C,D đúng
Đáp án : B