Cho tam giác ABC cân tại A, AC = 20cm,BC = 24cm. Các đường — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

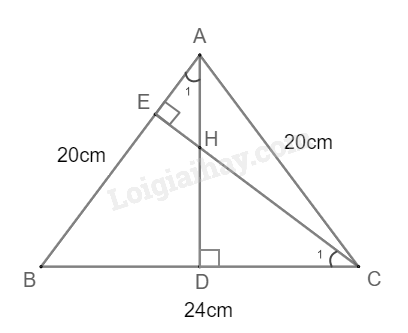
Tam giác ABC cân tại A nên \(BD = DC = \frac{{BC}}{2} = 12\left( {cm} \right)\)

Áp dụng định lý Pytago vào tam giác ADC vuông tại D ta có: \(A{D^2} = A{C^2} - D{C^2} = {16^2} \Rightarrow AD = 16cm\)

Tam giác CDH và tam giác ADB có: \(\widehat {CDH} = \widehat {ADB} = {90^0},\widehat {{C_1}} = \widehat {{A_1}}\) (cùng phụ với góc B)

Do đó, \(\Delta CDH \backsim \Delta ADB \Rightarrow \frac{{HD}}{{BD}} = \frac{{CD}}{{AD}} \Rightarrow \frac{{HD}}{{12}} = \frac{{12}}{{16}} = \frac{3}{4}\)

Suy ra: \(HD = 9cm\)