Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.

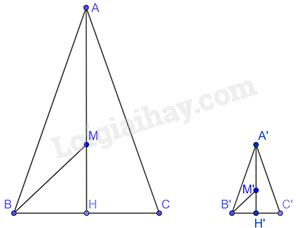
Tam giác ABC cân tại A, AH là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M thuộc AH. Do đó, \(3MH = AH\)

Tam giác A’B’C’ cân tại A’, A’H’ là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M’ thuộc A’H’. Do đó, \(3M'H' = A'H'\)

Xét tam giác ABH và tam giác A’B’H’ có: \(\widehat {AHB} = \widehat {A'H'B'} = {90^0},\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3\)

Suy ra: \(\Delta AHB \backsim \Delta A'H'B'\), do đó, \(\frac{{AH}}{{A'H'}} = 3 \Rightarrow \frac{{3HM}}{{3H'M'}} = 3 \Rightarrow \frac{{HM}}{{H'M'}} = 3\)

Tam giác BHM và tam giác B’H’M’ có:

\(\widehat {MHB} = \widehat {M'H'B'} = {90^0},\frac{{HM}}{{HM'}} = \frac{{BH}}{{B'H'}} = 3\)

Do đó, \(\Delta BMH \backsim \Delta B'M'H'\)  nên \(\frac{{BM}}{{B'M'}} = \frac{{BH}}{{B'H'}} = 3\)