Cho tam giác ABC cân tại A, đường cao CE. Biết rằng BE = — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

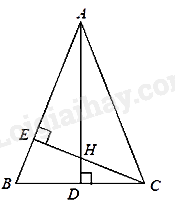
Kẻ đường cao AD của tam giác ABC.

Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến

Suy ra: \(BD = \frac{1}{2}BC = 4cm\)

Xét tam giác CBE và tam giác ABD có: \(\widehat {BEC} = \widehat {ADB} = {90^0}\) và góc B chung

Do đó, \(\Delta CBE \backsim \Delta ABD\left( {g.g} \right) \Rightarrow \frac{{BC}}{{AB}} = \frac{{BE}}{{BD}} \Rightarrow AB = \frac{{BD.BC}}{{BE}} = \frac{{32}}{3}\left( {cm} \right)\)