Cho \(\Delta ABC\) cân tại \(A\) ( \(\widehat A < 90^\circ \)). Kẻ \(BD \bot AC\)tại \(D\), kẻ \(CE \bot AB\)tại \(E\).
a) Chứng minh: \(\Delta ADE\)cân.
b) Chứng minh: \(DE//BC\) .
c) Gọi \(I\) l à giao điểm của \(BD\) và \(CE\). Chứng minh: \(IB = IC\) .
d) Chứng minh: \(AI \bot BC\) .
a) Chứng minh AD = AE nên tam giác ADE cân.
b) Chứng minh \(\widehat {AED} = \widehat {ABC}\) (hai góc đồng vị) nên DE // BC.
c) Chứng minh tam giác BIC cân tại I nên IB = IC.
d) Chứng minh A và I cùng thuộc đường trung trực của BC nên \(AI \bot BC\).
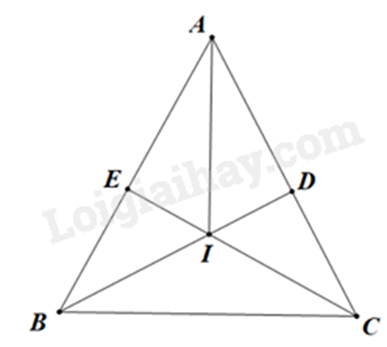
a) Xét \(\Delta ADB\)và \(\Delta AEC\), có:
\(\widehat A\): chung
\(AB = AC\)(vì \(\Delta ABC\)cân tại \(A\))
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \)(vì \(BD \bot AC\)tại \(D\) , \(CE \bot AB\) tại \(E\))
Suy ra \(\Delta ADB = \Delta ACE\)(cạnh huyền-góc nhọn).
Suy ra\(AD = AE\)(2 cạnh tương ứng).
Vậy \(\Delta ADE\)cân tại \(A\) .
b) Vì \(\Delta ABC\)cân tại \(A\) (gt)
Ta có: \(\widehat {ABC} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}\) (1)
Lại có: \(\Delta AED\) cân tại \(A\) (câu a)
Nên \(\widehat {AED} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}\) (2)
Từ (1) và (2) \( \Rightarrow \widehat {AED} = \widehat {ABC}\)
Mà \(\widehat {AED}\) và \(\widehat {ABC}\) ở vị trí đồng vị.
Vậy \(DE//BC\) .
c) Có tia \(BD\) nằm giữa hai tia \(BA,BC\).
Suy ra \(\widehat {ABD} + \widehat {DBC} = \widehat {ABC}\)
Suy ra \(\widehat {DBC} = \widehat {ABC} - \widehat {ABD}\)
Tương tự, có:
\(\widehat {ECB} = \widehat {ACB} - \widehat {ACE}\)
Mà \(\widehat {ABC} = \widehat {ACB}\) (do \(\Delta ABC\)cân tại \(A\) )
\(\widehat {ADB} = \widehat {ACE}\) ( vì \(\Delta ADB = \Delta AEC\) )
Suy ra \(\widehat {DBC} = \widehat {ECB}\)
Vậy \(\Delta IBC\) cân tại \(I\).
Suy ra \(IB = IC\)
d) Có: \(AB = AC\) (vì \(\Delta ABC\)cân tại \(A\))
Do đó\(A\) thuộc đường trung trực của \(BC\)
Lại có: \(IB = IC\)(câu c)
Suy ra \(I\) thuộc đường trung trực của \(BC\)
Suy ra \(AI\) là đường trung trực của \(BC\)
Suy ra \(AI \bot BC\).