Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a) Chứng minh \(\Delta ABE = \Delta ACD\).
b) Tứ giác BDEC là hình gì? Vì sao?
c) Các điểm D, E ở vị trí nào thì BD = DE = EC?
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh góc cạnh.
b) Chứng minh BDEC có một cặp cạnh đối song song nên là hình thang.
Chứng minh hai cạnh bên BD = CE nên BDEC là hình thang cân.
c) Dựa vào BD = DE và DE = EC suy ra tam giác BDE và tam giác DEC cân, suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) và \(\widehat {{C_1}} = \widehat {{C_2}}\).
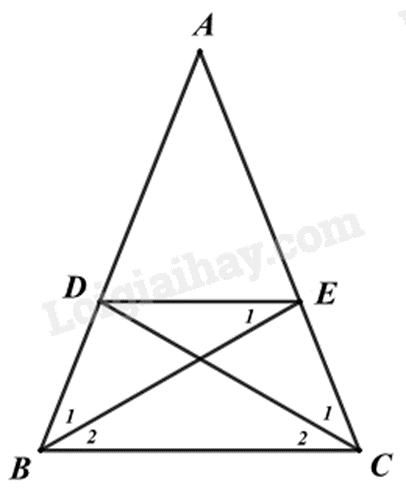
a) Xét tam giác ABE và ACD có:
\(AB = AC\) (tam giác ABC cân tại A)
\(\widehat A\) chung
\(AE = AD\) (gt)
Suy ra \(\Delta ABE = \Delta ACD\left( {c.g.c} \right)\) (đpcm)
b) Vì AD = AE nên tam giác ADE cân tại A, suy ra \(\widehat {ADE} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân)
Tam giác ABC cân tại A, suy ra \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân)
Suy ra \(\widehat {ADE} = \widehat {ABC}\).
Mà hai góc này ở vị trí đồng vị nên DE // BC (cặp góc đồng vị bằng nhau)
Do đó BDEC là hình thang.
Ta có: AB = AC, AD = AE suy ra AB – AD = AC – AE hay BD = CE.
Suy ra BDEC là hình thang cân (hình thang có hai cạnh bên bằng nhau).
c) Theo đề bài, ta có BD = DE = EC.
Tam giác BDE có BD = DE nên tam giác BDE cân tại D. Suy ra \(\widehat {{B_1}} = \widehat {{E_1}}\)
Mà \(\widehat {{E_1}} = \widehat {{B_2}}\) (hai góc so le trong)
Suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) hay BE là tia phân giác của \(\widehat {ABC}\).
Tương tự, ta chứng minh được \(\widehat {{C_1}} = \widehat {{C_2}}\) hay CD là tia phân giác của \(\widehat {ACB}\).
Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC.