Cho tam giác ABC cân tại $A. $ Trên $BC$ lấy hai điểm $D$ — Không quảng cáo

Phương pháp giải

Áp dụng hai định lý:

- Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn

- Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

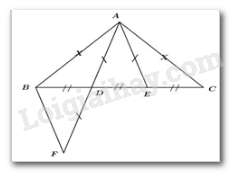
Xét \(\Delta ABD\) và \(\Delta ACE\) có:

$AB = AC$ (gt)

\(\widehat B = \widehat C\) (tính chất tam giác cân)

\(BD = EC\left( {gt} \right)\)

\( \Rightarrow \Delta ABD = \Delta ACE\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BAD} = \widehat {CAE}\) (2 góc tương ứng) nên A đúng.

Trên tia đối của tia $DA$  lấy điểm $F$  sao cho \(AD = DF\).

Xét \(\Delta ADE\) và \(\Delta FDB\) có:

\(AD = DF\left( {gt} \right)\)

\(\widehat {ADE} = \widehat {BDF}\) (đối đỉnh)

\(BD = DE\left( {gt} \right)\)

$ \Rightarrow \Delta ADE = \Delta FDB\left( {c - g - c} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {DAE} = \widehat {BFD}\\AE = BF\end{array} \right.$

Ta có: \(\widehat {AEC} = \widehat B + \widehat {BAD}\) (tính chất góc ngoài của tam giác)

\( \Rightarrow \widehat {AEC} > \widehat B = \widehat C\) nên trong \(\Delta AEC\) suy ra \(AE < AC\) (quan hệ giữa góc và cạnh trong tam giác)

Mà \(\left\{ \begin{array}{l}AB = AC\left( {gt} \right)\\BF = AE\left( {cmt} \right)\end{array} \right. \Rightarrow BF < AB\)

Xét \(\Delta ABF\) có: \(BF < AB\left( {cmt} \right)\) suy ra \(\widehat {BFA} > \widehat {FAB}\) (quan hệ giữa cạnh và góc trong tam giác)

Vậy \(\widehat {BAD} = \widehat {CAE} < \widehat {DAE}\) nên B, C đúng.

Vậy cả A, B, C đều đúng.