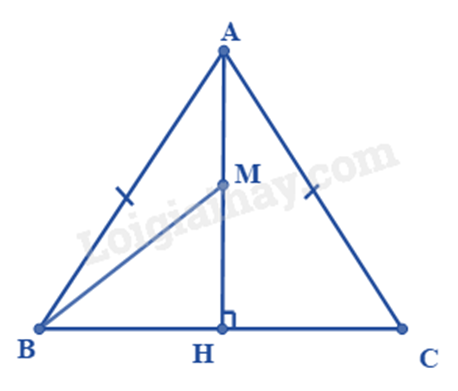
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:
a) BH = CH.
b) BA > BM.
a) Chứng minh \(\Delta AHB = \Delta AHC\) nên \(BH = CH\).
b) Sử dụng quan hệ giữa đường vuông góc và đường xiên để chứng minh.
a) Xét \(\Delta AHB\) và \(\Delta AHC\) có:
\(\widehat {AHB} = \widehat {AHC} = {90^0}\)
\(AB = AC\) (\(\Delta ABC\) cân tại A)
AH chung
Suy ra \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông)
Suy ra \(BH = CH\) (hai cạnh tương ứng) (đpcm)
b) Do M nằm giữa A và H nên HA > HM.
Ta có BH là đường vuông góc, BA và BM là các đường xiên kẻ từ B đến đường thẳng AH nên HM là hình chiếu của BM, HA là hình chiếu của AB xuống AH.
Vì HA > HM nên BA < BM.
Vậy BA > BM (đpcm).