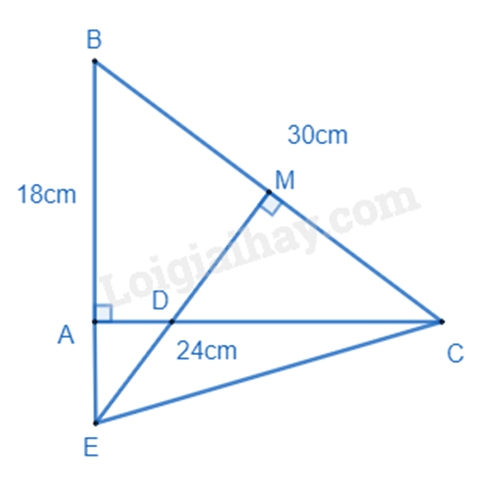
Cho \(\Delta ABC\) có AB = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt AC, AB lần lượt tại D, E.
a) Chứng minh rằng $\Delta ABC\backsim \Delta MDC$.
b) Tính độ dài các cạnh của \(\Delta MDC\).
c) Tính độ dài BE, EC.
a) Sử dụng định lí Pythagore đảo để chứng minh \(\Delta ABC\) vuông.
Chứng minh $\Delta ABC\backsim \Delta MDC\left( g.g \right)$
b) Vì M là trung điểm của BC nên tính được MC.
Từ phần a có $\Delta ABC\backsim \Delta MDC$ suy ra tỉ số của các cặp cạnh tương ứng trong hai tam giác để tính MD và CD.
c) Chứng minh $\Delta BME\backsim \Delta BAC\left( g.g \right)$, tính được BE.
Chứng minh \(\Delta BME = \Delta CME\left( {c.g.c} \right)\) suy ra CE.
a) Xét \(\Delta ABC\) có: \(A{B^2} + A{C^2} = {18^2} + {24^2} = 900 = {30^2} = B{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại A (định lí Pythagore đảo)
Xét \(\Delta ABC\) và \(\Delta MDC\), ta có:
\(\widehat A = \widehat M\left( { = {{90}^0}} \right)\)
\(\widehat C\) chung
$\Rightarrow \Delta ABC\backsim \Delta MDC\left( g.g \right)$ (đpcm)
b) Ta có: M là trung điểm của BC nên \(BM = CM = \frac{1}{2}BC = \frac{1}{2}.30 = 15\left( {cm} \right)\)
Vì $\Delta ABC\backsim \Delta MDC$ nên ta có:
\(\frac{{AB}}{{MD}} = \frac{{BC}}{{CD}} = \frac{{AC}}{{MC}}\)
\(\frac{{18}}{{MD}} = \frac{{30}}{{CD}} = \frac{{24}}{{15}} = \frac{8}{5}\)
\( \Rightarrow MD = 18:\frac{8}{5} = 11,25\)
\(CD = 30:\frac{8}{5} = 18,75\)
c) Xét \(\Delta BME\) và \(\Delta BAC\) có:
\(\widehat M = \widehat A\left( { = {{90}^o}} \right)\)
\(\widehat B\) chung
$\Rightarrow \Delta BME\backsim \Delta BAC\left( g.g \right)$
\( \Rightarrow \frac{{BE}}{{BC}} = \frac{{BM}}{{AB}}\)
\(\frac{{BE}}{{30}} = \frac{{15}}{{18}} = \frac{5}{6} \Rightarrow BE = \frac{5}{6}.30 = 25\left( {cm} \right)\)
Xét \(\Delta BME\) và \(\Delta CME\) có:
BM = CM (M là trung điểm của BC)
\(\widehat {BME} = \widehat {CME}\left( { = {{90}^0}} \right)\)
ME chung
\( \Rightarrow \Delta BME = \Delta CME\left( {c.g.c} \right)\)
\( \Rightarrow BE = CE = 25cm\).