Đề bài
Cho tam giác ABC có AB = 24cm; AC = 36cm. Kẻ BD \(\left( {A \in AC} \right)\) góc với tia phân giác của góc A tại H. Gọi M là trung điểm của BC. Độ dài đoạn thẳng HM là:
-
A.
6cm
-
B.
12cm
-
C.
3cm
-
D.
8cm
Phương pháp giải
Chứng minh HM là đường trung bình của tam giác BDC.
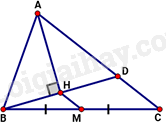
Vì AH là tia phân giác của goác BAC, AH vuông góc BD nên tam giác cân tại A.
\( \Rightarrow AB = A{\rm{D}} = 24cm\)
Do tam giác ABD cân tại A nên AH là đường phân giác đồng thời là đường trung tuyến của tam giác ABD
Suy ra H là trung điểm của BD
Ta có: DC = AC – AD = 36 – 24 = 12cm
Xét tam giác BDC, ta có H là trung điểm của BD , M là trung điểm của BC nên HM là đường trung bình của tam giác BDC
\( \Rightarrow HM = \frac{1}{2}DC = \frac{1}{2}.12 = 6cm\)
Đáp án : A