Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc — Không quảng cáo

Phương pháp giải

Chứng minh $\Delta ACB \backsim \Delta ECA$ (c-g-c) suy ra $\hat B = \widehat {CAE}$ tức là $\hat B = \frac{{\hat A}}{2}$

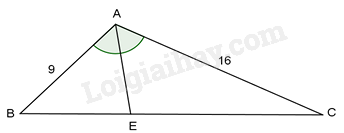
Kẻ đường phân giác AE của $\Delta ABC$ . Theo tính chất đường phân giác, ta có:

$\frac{{BE}}{{EC}} = \frac{{AB}}{{AC}} = \frac{9}{{16}}$ hay $\frac{{BE}}{{AB}} = \frac{{CE}}{{AC}}$

Nên $\frac{{BE + EC}}{{AB+AC}} = \frac{{20}}{{9+16}}=\frac{4}{5}$

Hay $\frac{{CE}}{{AC}} = \frac{{CE}}{{16}} =\frac{4}{5} \Rightarrow EC = 12,8(cm)$

Xét $\Delta ACB$ và $\Delta ECA$ có: $\hat C$ là góc chung

$\frac{{AC}}{{EC}} = \frac{{CB}}{{CA}}$ (vì $\frac{{16}}{{12,8}} = \frac{{20}}{{16}})$

Do đó $\Delta ACB \backsim \Delta ECA$ (c-g-c) suy ra $\hat B = \widehat {CAE}$ tức là $\hat B = \frac{{\hat A}}{2}$