Đề bài
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.
-
A.
6cm.
-
B.
5cm.
-
C.
4cm.
-
D.
7cm.
Phương pháp giải
Sử dụng định lí Thales để chứng minh.
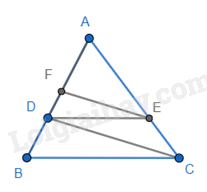
Ta có: DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{6}{9} = \frac{2}{3}\) (định lí Thales)
EF // CD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\) (định lí Thales)
\( \Rightarrow AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\).
Đáp án : C