Cho tam giác ABC có AB < AC. Cho M là trung điểm của cạnh BC. Tia phân giác của góc A cắt đường thẳng qua M, vuông góc với BC tại điểm I. Qua I kẻ IH vuông góc với AB, IK vuông góc với AC ( H \( \in \) đường thẳng AB, K \( \in \) đường thẳng AC). Phát biểu nào sau đây sai:
-
A.
IH = IK
-
B.
\(AK = \frac{{AB + AC}}{2}\)
-
C.
\(MI = \frac{{HI + KI}}{4}\)
-
D.
BH = CK
Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau
Cộng, trừ đoạn thẳng suy ra các đẳng thức
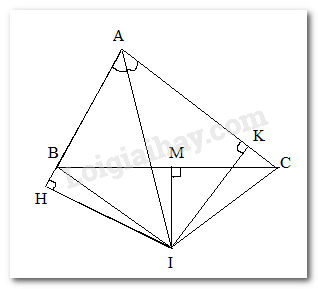
Xét tam giác vuông AIH và AIK có:
AI chung
\(\widehat {HAI} = \widehat {KAI}\) ( do AI là tia phân giác của góc BAC)
\( \Rightarrow \Delta AIH = \Delta AIK\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) AH = AK ; IH = IK ( các cạnh tương ứng) nên A đúng
Xét tam giác vuông MBI và MCI có:
MB = MC ( do M là trung điểm của BC)
\(\widehat {BMI} = \widehat {CMI}( = 90^\circ )\)
MI chung
\( \Rightarrow \)\(\Delta MBI = \Delta MCI\) ( c.g.c)
\( \Rightarrow \) BI = CI ( 2 cạnh tương ứng)
Xét tam giác vuông HBI và KCI có:
BI = CI ( cmt)
HI = KI ( cmt)
\( \Rightarrow \)\(\Delta HBI = \Delta KCI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) HB = KC ( 2 cạnh tương ứng) nên D đúng
Ta có:
AB + AC = (AH – HB) + (AK + KC) = AK – KC + AK + KC = 2.AK ( vì AH = AK, HB = KC)
\( \Rightarrow AK = \frac{{AB + AC}}{2}\) nên B đúng
Đáp án : C