Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt — Không quảng cáo

Phương pháp giải

Sử dụng tính chất tia phân giác, tính chất hai góc kề bù và định lý tổng ba góc trong tam giác.

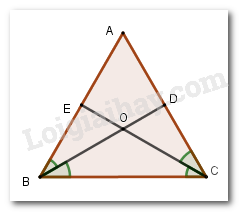
Vì \(BD\) và \(CE\) là tia phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) nên \(\widehat {ABD} = \widehat {CBD}\) và \(\widehat {ACE} = \widehat {BCE}.\)

Xét tam giác \(ABD\) và tam giác \(CBD\) có:

+ \(AB = AC\,\left( {gt} \right)\)

+ \(\widehat {ABD} = \widehat {CBD}\) (cmt)

+ Cạnh \(BD\) chung

Suy ra  \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BCA} = \widehat {BAC}\) (hai góc tương ứng) (1)

Tương tự ta có \(\Delta BCE = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {CBA} = \widehat {BAC}\) (hai góc tương ứng) (2)

Từ (1) và (2) ta có \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB}\). Mà \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (định lý tổng ba góc của tam giác) nên \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = \frac{{180^\circ }}{3} = 60^\circ .\)

Lại có \(\widehat {ABD} = \widehat {CBD}\) (cmt) nên \(\widehat {CBO} = \frac{{\widehat {ABC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \); \(\widehat {ACE} = \widehat {BCE} = \frac{{\widehat {ACB}}}{2} = \frac{{60^\circ }}{2} = 30^\circ .\)

Xét tam giác \(BOC\) có \(\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ \) (định lý tổng ba góc của một tam giác)

Nên \(\widehat {BOC} = 180^\circ  - 30^\circ  - 30^\circ  = 120^\circ .\)

Vậy \(\widehat {BOC} = 120^\circ .\)