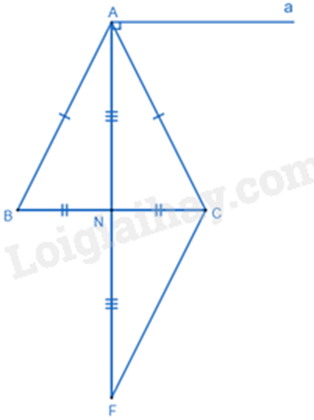
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
a) Dựa vào các trường hợp bằng nhau của hai tam giác.
b) Chứng minh \(AN \bot BC\) suy ra a // BC.
c) Dựa vào bất đẳng thức tam giác để chứng minh.
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có:
\(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\)
Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm)
b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\).
Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\).
Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt)
Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm).
c) Xét \(\Delta ABN\) và \(\Delta FCN\) có:
\(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\)
\(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh)
Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm)
Suy ra AB = CF.
Xét \(\Delta ACF\) có:
\(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\)
(vì AB = CF và AF = 2AN) (đpcm).