Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
-
A.
\(BE = CD\)
-
B.
\(BK = KC\)
-
C.
\(BD = CE\)
-
D.
\(DK = KC\)
Chứng minh 2 tam giác bằng nhau rồi dựa vào tính chất hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.
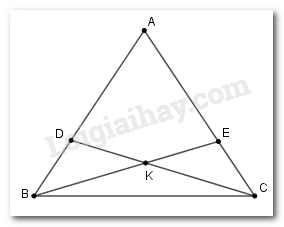
Xét tam giác \(ABE\) và tam giác \(ADC\) có
+ \(AD = AE\left( {gt} \right)\)
+ Góc \(A\) chung
+ \(AB = AC\left( {gt} \right)\)
\( \Rightarrow \) \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và \(BE = CD\) (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = 180^\circ \); \(\widehat {AEB} + \widehat {BEC} = 180^\circ \) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
\( \Rightarrow \)\(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;\,AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nên C đúng.
Xét tam giác \(KBD\) và tam giác \(KCE\) có
\(\widehat {ABE} = \widehat {ACD}\,\left( {cmt} \right)\)
\(BD = EC\,\left( {cmt} \right)\)
\(\widehat {BDC} = \widehat {BEC}\,\left( {cmt} \right)\)
\( \Rightarrow \) \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\)
\( \Rightarrow KB = KC;\,KD = KE\) (hai cạnh tương ứng) nên B đúng, D sai.
Đáp án : D