Cho tam giác ABC có AC — Không quảng cáo

Phương pháp giải

Chứng minh EI, FI là các đường trung bình của tam giác => EI = FI => tam giác FDE cân tại I, ta tính được số đo góc BEF.

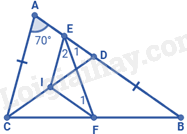
Xét tam giác ADC có E là trung điểm của AD, I là trung điểm của CD

Suy ra: EI là đường trung bình của tam giác ADC

$\Rightarrow EI//AC$

$\Rightarrow \widehat {IE{\rm{D}}} = \widehat A = {70^o}$ (đồng vị) và $EI = \frac{{AC}}{2}$

Tương tự: FI là đường trung bình của tam giác CBD

Suy ra FI //BD; $FI = \frac{{B{\rm{D}}}}{2}$

$\Rightarrow \widehat {{F_1}} = \widehat {{E_1}}$ (hai góc so le trong bằng nhau)

Lại có: AC = BD (giả thiết), suy ra EI = FI

Suy ra tam giác FDE cân tại I

$\widehat {{F_2}} = \widehat {{E_1}}$

$\Rightarrow \widehat {{E_1}} = \widehat {{E_2}} = \frac{1}{2}\widehat {IE{\rm{D}}} = \frac{1}{2}.\widehat A = \frac{1}{2}.70 = {35^o}$