Cho tam giác ABC có BA = BC = a,AC = b. Đường phân giác góc — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

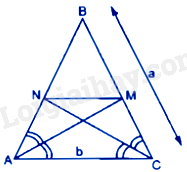
Xét tam giác ABC có AM là đường phân giác góc BAC nên \(\frac{{MB}}{{MC}} = \frac{{AB}}{{AC}} = \frac{a}{b}\)

Xét tam giác ABC có CN là đường phân giác góc BCA nên \(\frac{{NB}}{{NA}} = \frac{{CB}}{{AC}} = \frac{a}{b}\)

Do đó, \(\frac{{NB}}{{NA}} = \frac{{MB}}{{MC}}\) nên MN//AC (định lý Thalès đảo)

Ta có: \(\frac{{NB}}{{NA}} = \frac{{CB}}{{AC}} = \frac{a}{b} \Rightarrow \frac{{NB}}{{NB + NA}} = \frac{a}{{a + b}}\) hay \(\frac{{NB}}{{AB}} = \frac{a}{{a + b}}\)

Do đó, \(NB = \frac{{{a^2}}}{{a + b}}\)

Lại có: MN//AC nên \(\frac{{MN}}{{AC}} = \frac{{NB}}{{AB}}\) , do đó \(MN = \frac{{AC.NB}}{{AB}} = \frac{{ab}}{{a + b}}\)