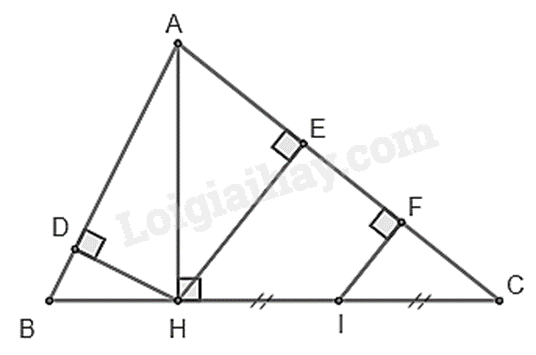
Cho \(\Delta ABC\) có ba góc nhọn (AB < AC). Kẻ đường cao AH, từ H kẻ HD và HE lần lượt vuông góc với AB và AC (\(D \in AB,E \in AC\)).
a) Chứng minh $\Delta AHD\backsim \Delta ABH$.
b) Chứng minh AD.AB = AE.AC.
c) Gọi I là trung điểm của HC. Điểm F là chân đường vuông góc hạ từ I đến AC.
Chứng minh \(C{A^2} - H{C^2} = A{F^2} - C{F^2}\)
a) Chứng minh tam giác AHD và tam giác ABH đồng dạng theo trường hợp góc – góc.
b) Chứng minh $\Delta AHE\backsim \Delta ACH$ suy ra \(A{H^2} = AE.AC\)
Dựa vào ý a suy ra \(A{H^2} = AB.AD\), ta được điều phải chứng minh.
c) Dựa vào định lí Pythagore suy ra \(C{A^2} - H{C^2} = A{H^2}\).
Chứng minh F là trung điểm của EC.
Sử dụng hằng đẳng thức hiệu hai bình phương để suy ra \(A{F^2} - C{F^2} = A{H^2}\).
Ta được điều phải chứng minh.
a) Xét \(\Delta AHD\) và \(\Delta ABH\) có:
\(\widehat {ADH} = \widehat {BHA} = {90^0}\)
\(\widehat {BAH}\) chung
nên $\Delta AHD\backsim \Delta ABH\left( g.g \right)$ (đpcm)
b) Xét \(\Delta AHE\) và \(\Delta ACH\) có:
\(\widehat {AEH} = \widehat {AHC} = {90^0}\)
\(\widehat {HAC}\) chung
nên $\Delta AHE\backsim \Delta ACH\left( g.g \right)$
Suy ra \(\frac{{AE}}{{AH}} = \frac{{AH}}{{AC}}\). Do đó \(A{H^2} = AE.AC\) (1)
$\Delta AHD\backsim \Delta ABH\left( cmt \right)$ suy ra \(\frac{{AD}}{{AH}} = \frac{{AH}}{{AB}}\). Do đó \(A{H^2} = AB.AD\) (2)
Từ (1) và (2) suy ra \(AB.AD = AC.AE\) (đpcm)
c) Áp dụng định lí Pythagore vào tam giác vuông ACH, ta có:
\(C{A^2} - H{C^2} = A{H^2}\) (3)
Xét tam giác CHE có:
I là trung điểm của CH
\(FI//EH\left( {FI \bot AC,HE \bot AC} \right)\)
nên FI là đường trung bình của tam giác CHE.
Suy ra F là trung điểm của CE hay EF = FC.
Áp dụng hằng đẳng thức hiệu hai bình phương, ta có:
\(\begin{array}{l}A{F^2} - C{F^2} = \left( {AF - CF} \right)\left( {AF + CF} \right)\\ = \left( {AF - EF} \right).AC\\ = AE.AC = A{H^2}\,(4)\end{array}\)
Từ (3) và (4) suy ra \(C{A^2} - H{C^2} = A{F^2} - C{F^2}\). (đpcm)