Cho tam giác ABC có ba góc nhọn. Đường cao AF, BE cắt nhau — Không quảng cáo

Phương pháp giải

a) Chứng minh AHBK có hai cặp cạnh đối song song nên là hình bình hành.

b) Chứng minh $\Delta HAE\backsim \Delta HBF$ theo trường hợp góc – góc.

c) Chứng minh $\Delta AFC\backsim \Delta BEC$ (g.g) để chứng minh $CE.CA = CF.CB$.

d) Gọi D là giao điểm KH và AB

Để tứ giác AHBK là hình thoi thì KH vuông góc AB

Ta có: H là trực tâm $\Rightarrow$ CH vuông góc AB

$\Rightarrow$ C, H, D thẳng hàng $\Rightarrow$ CD là đường cao và D là trung điểm của AB $\Rightarrow$ CD cũng là đường trung tuyến

$\Rightarrow$ Tam giác ABC cân tại C

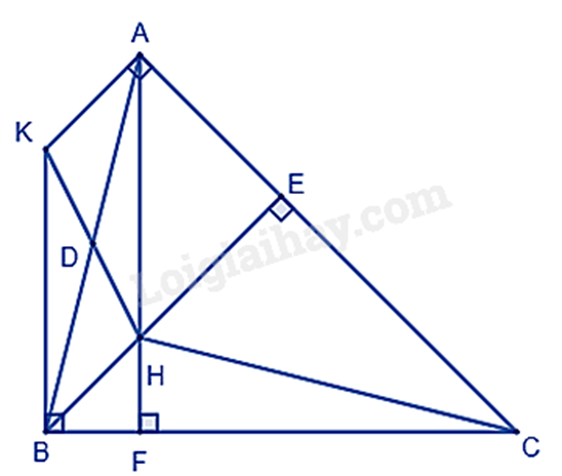
a) Ta có:

$\left. \begin{array}{l}AK \bot AC\\BE \bot AC\end{array} \right\} \Rightarrow AK//BE$

$\left. \begin{array}{l}BK \bot BC\\AF \bot BC\end{array} \right\} \Rightarrow BK//AF$

Xét tứ giác AHBK có:

$\begin{array}{l}AK//BH\left( {H \in BE} \right)\\AB//AH\left( {H \in AF} \right)\end{array}$

$\Rightarrow$ AHBK là hình bình hành.

b) Xét $\Delta HAE$ và $\Delta HBF$ có:

$\widehat E = \widehat F\left( { = {{90}^0}} \right)$

$\widehat {AHE} = \widehat {BHF}$ (hai góc đối đỉnh)

$\Rightarrow \Delta HAE\backsim \Delta HBF$ (g.g) (đpcm)

c) Xét $\Delta AFC$ và $\Delta BEC$ có:

$\widehat F = \widehat E\left( { = {{90}^0}} \right)$

$\widehat C$ chung

$\Rightarrow \Delta AFC\backsim \Delta BEC\left( g.g \right)$

$\Rightarrow \frac{{AC}}{{BC}} = \frac{{CF}}{{CE}} \Rightarrow AC.CE = CF.CB$ (đpcm)

d) Gọi D là giao điểm của AB và HK $\Rightarrow$ D là trung điểm của AB và HK.

Để AHBK là hình thoi thì $AB \bot HK$.

Mà H trực tâm của tam giác ABC nên $CH \bot AB$.

$\Rightarrow$ C, H, K thẳng hàng hay C, H, D thẳng hàng.

Khi đó CD là đường cao của tam giác ABC.

Mà D là trung điểm của AB nên CD cũng là đường trung tuyến của tam giác ABC

$\Rightarrow$ Tam giác ABC cân tại C.

Vậy để AHBK là hình thoi thì tam giác ABC cân tại C.