Cho tam giác ABC có BC = 20cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K kẻ các đường EF và MN song song với BC (E, M \( \in \) AB, F, N \( \in \) AC).
a) Tính độ dài các đoạn MN và EF.
b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là \(300c{m^2}\).
a) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa MN, EF với BC.
b) Tính độ dài AH qua công thức tính diện tích tam giác. Từ đó suy ra AK.
Chứng minh MNFE là hình thang, KI là đường cao của hình thang MNFE.
Sử dụng công thức tính diện tích hình thang.
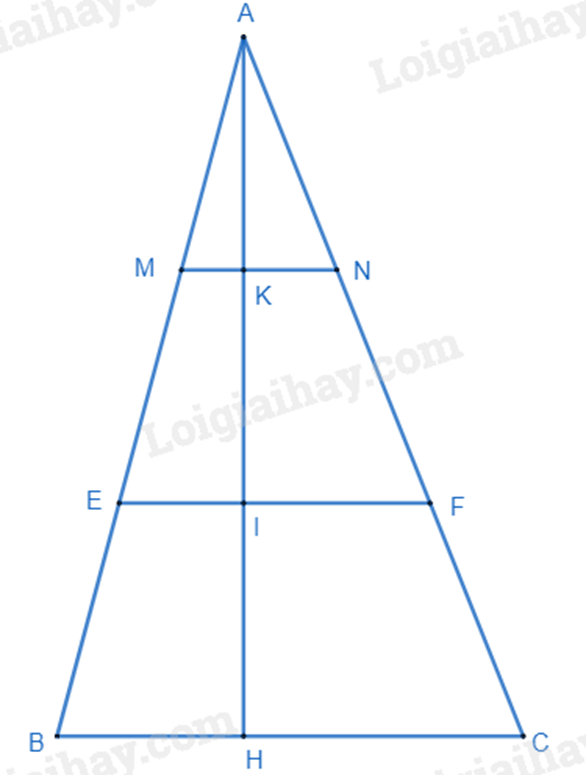
a) Theo bài ra ta có \(AK = KI = IH\)\( \Rightarrow \frac{{AK}}{{AH}} = \frac{1}{3};\frac{{AI}}{{AH}} = \frac{2}{3}\).
Áp dụng hệ quả của định lí Thales vào tam giác ABH có MK // BH và EI // BH
\( \Rightarrow \frac{{MK}}{{BH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{EI}}{{BH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (1)
Áp dụng hệ quả của định lí Thales vào tam giác ACH có NK // CH và FI // CH
\( \Rightarrow \frac{{NK}}{{CH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{FI}}{{CH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (2)
Từ (1) và (2), áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{{MK}}{{BH}} = \frac{{NK}}{{CH}} = \frac{{MK + NK}}{{BH + CH}} = \frac{{MN}}{{BC}} = \frac{1}{3}\)\( \Rightarrow MN = \frac{1}{3}BC = \frac{{20}}{3}\left( {cm} \right)\)
\(\frac{{EI}}{{BH}} = \frac{{FI}}{{CH}} = \frac{{EI + FI}}{{BH + CH}} = \frac{{EF}}{{BC}} = \frac{2}{3}\)\( \Rightarrow EF = \frac{2}{3}BC = \frac{2}{3}.20 = \frac{{40}}{3}\left( {cm} \right)\)
b) Diện tích tam giác ABC là \(300c{m^2}\)
\(\begin{array}{l} \Rightarrow \frac{1}{2}AH.BC = 300\\\frac{1}{2}AH.20 = 300\\ \Rightarrow AH = 300:\frac{{20}}{2} = 30\left( {cm} \right)\end{array}\)
Ta có: \(\frac{{AK}}{{AH}} = \frac{1}{3} \Rightarrow AK = \frac{1}{3}AH = \frac{1}{3}.30 = 10\left( {cm} \right)\) \( \Rightarrow \) KI = AK = 10 cm.
Vì MN và EF cùng song song với BC nên MNFE là hình thang. Vì \(AH \bot BC \Rightarrow AH \bot MN\) và \(AH \bot EF\)
\( \Rightarrow KI\) là đường cao của hình thang MNFE \(\left( {K \in MN;I \in EF} \right)\).
Diện tích hình thang MNFE là:
\({S_{MNFE}} = \frac{1}{2}\left( {MN + EF} \right).KI = \frac{1}{2}.\left( {\frac{{20}}{3} + \frac{{40}}{3}} \right).10 = 100\left( {c{m^2}} \right)\)
Vậy \({S_{MNFE}} = 100c{m^2}\).