Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H — Không quảng cáo

Phương pháp giải

Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán.

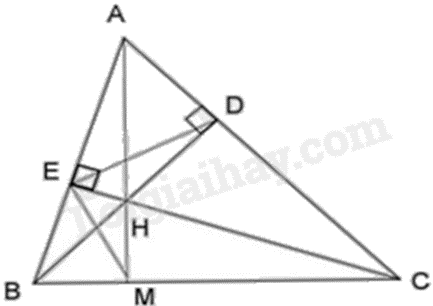
a) Xét $\Delta HBE$ và $\Delta HCD$ có:

$\widehat {BDC} = \widehat {CEB} = {90^0}$

$\widehat {EHB} = \widehat {DHC}$ (2 góc đối đỉnh)

Suy ra $\Delta HBE\backsim \Delta HCD\left( g-g \right)$ (điều phải chứng minh)

b) Theo câu a) ta có: $\Delta HBE\backsim \Delta HCD$ suy ra $\frac{{HE}}{{HD}} = \frac{{HB}}{{HC}}$ hay $\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}$

Xét $\Delta HED$ và $\Delta HBC$ ta có:

$\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}$ (cmt)

$\widehat {EHD} = \widehat {BHC}$ (hai góc đối đỉnh)

$\widehat {HDE} = \widehat {HAE}$

Suy ra $\Delta HED\backsim \Delta HBC\left( c-g-c \right).$

Mà đường cao ${\rm{BD}}$ và ${\rm{CE}}$ cắt nhau tại ${\rm{H}}$ (theo giả thiết)

Suy ra H là trực tâm của $\Delta ABC$ hay $AH \bot BC$ tại M suy ra $\widehat {AMB} = {90^ \circ }$.

Xét $\Delta AMB$ và $\Delta CEB$ có:

$\widehat {CEB} = \widehat {AMB} = {90^0}$

$\widehat B$ chung

Suy ra $\Delta AMB\backsim \Delta CEB\left( g-g \right)$

Suy ra $\widehat {MAB} = \widehat {ECB}$ hay $\widehat {HAE} = \widehat {HCB}$ (2)

Từ (1) và (2) ta có: $\widehat {HDE} = \widehat {HAE}$ (điều phải chứng minh)