Đề bài
Cho tam giác \(ABC\) có đường cao \(AH.\) Biết \(AC = 15\;\;{\rm{cm}},\,\,AH = 12\;\;{\rm{cm,}}\,\,BH = 9\;\;{\rm{cm}}.\) Hỏi tam giác \(ABC\) là tam giác gì?
-
A.
Tam giác vuông.
-
B.
Tam giác cân.
-
C.
Tam giác đều.
-
D.
Tam giác tù.
Phương pháp giải
Sử dụng định lí Pythagore trong tam giác vuông để tính.
Chứng minh tam giác ABC có đường cao đồng thời là đường trung tuyến.
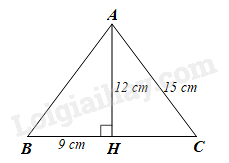
Xét \(\Delta AHC\) vuông tại \(H\), theo định lí Pythagore ta có:
\(C{H^2} = A{C^2} - A{H^2} = {15^2} - {12^2} = 81\).
Do đó \(CH = \sqrt {81} = 9\;\;{\rm{cm}}\)
Suy ra \(BH = CH = 9\;\;{\rm{cm}}\) hay \(H\) là trung điểm của \(BC\)
Tam giác \(ABC\) có đường cao \(AH\) đồng thời là đường trung tuyến nên \(\Delta ABC\) cân tại \(A\).
Đáp án B.
Đáp án : B