Đề bài
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E.
Chọn đáp án đúng.
-
A.
\(\frac{{EC}}{{EA}} = \frac{1}{3}.\frac{{DM}}{{DA}}\)
-
B.
\(\frac{{EC}}{{EA}} = 3\frac{{DM}}{{DA}}\)
-
C.
\(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\)
-
D.
\(\frac{{EC}}{{EA}} = \frac{1}{2}.\frac{{DM}}{{DA}}\)
Phương pháp giải
Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
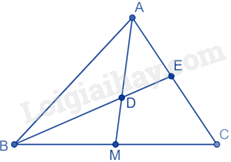
Xét tam giác ABC có BE là đường phân giác của góc ABC nên \(\frac{{EC}}{{EA}} = \frac{{BC}}{{BA}}\) (1)
Xét tam giác ABM có DB là đường phân giác của góc ABM nên \(\frac{{DM}}{{DA}} = \frac{{BM}}{{BA}}\) (2)
Mà M là trung điểm của BC nên \(BM = MC = \frac{1}{2}BC \Rightarrow \frac{{DM}}{{DA}} = \frac{{BM}}{{BA}} = \frac{{BC}}{{2.BA}}\)
Nên \(2\frac{{DM}}{{DA}} = \frac{{BC}}{{BA}}\) (3)
Từ (1), (2) và (3) ta có: \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\) .
Đáp án : C