Cho tam giác ABC có hai đường trung tuyến BD;CE sao cho BD — Không quảng cáo

Phương pháp giải

+ Sử dụng tính chất về đường trung tuyến của tam giác

+ Chứng minh hai tam giác bằng nhau \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\)

+ Từ đó suy ra tính chất của tam giác \(ABC.\)

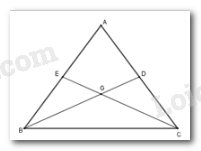
Hai đường trung tuyến \(BD;CE\) cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ABC.\)

\(\Rightarrow\) \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) mà \(BD = CE \Rightarrow \)\(BG = CG.\)

Ta được: \(BD - BG = CE - CG \Rightarrow GD = GE\)

Xét \(\Delta BGE\) và \(\Delta CGD\) có

+ \(BG = CG\)

+ \(\widehat {BGE} = \widehat {CGD}\)  (đối đỉnh)

+ \(GD = GE\)

Nên \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\)

\(\Rightarrow\) \(BE = CD \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}AC\) do đó \(AB = AC\) hay tam giác $ABC$ cân tại \(A.\)