Đề bài
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng \(AB + AC > 2AM\).
Phương pháp giải
Dựa vào kiến thức về đường trung tuyến trong tam giác.
Lấy điểm D thuộc tia đối của tia AM sao cho AM = DM.
Chứng minh \(\Delta AMB = \Delta DMC\) suy ra \(AB = CD\).
Sử dụng bất đẳng thức tam giác để chứng minh \(AB + AC > AD = 2AM\).
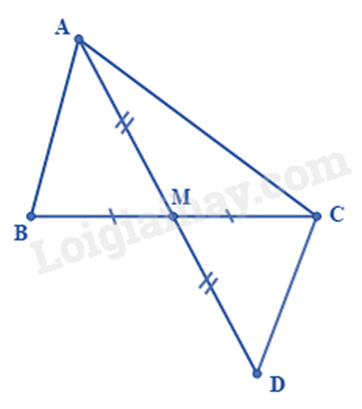
Do AM là trung tuyến của tam giác ABC nên ta có BM = CM.
Trên tia đối của tia AM lấy điểm D sao cho AM = DM.
Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(AM = DM\)
\(BM = CM\)
\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh)
Suy ra \(\Delta AMB = \Delta DMC\) (c.g.c) suy ra AB = CD (hai cạnh tương ứng)
Khi đó \(AB + AC = DC + AC > AD\) (bất đẳng thức tam giác)
Mà AM = DM nên AD = 2.AM
Do đó: \(AB + AC > 2AM\).