Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
-
A.
\(BI = IK > KE\)
-
B.
\(BI > IK > KE\)
-
C.
\(BI = IK = KE\)
-
D.
\(BI < IK < KE\)
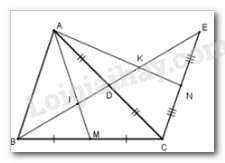
\(I\) là trọng tâm tam giác \(ABC\) nên \(BI = \dfrac{2}{3}BD = \dfrac{1}{3}BE\) \(\left( 1 \right)\)
\(K\) là trọng tâm tam giác \(ACE\) nên \(EK = \dfrac{2}{3}ED = \dfrac{1}{3}BE\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(IK = \dfrac{1}{3}BE\) từ đó \(BI = EK = IK\) .
Đáp án : C