Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam — Không quảng cáo

Phương pháp giải

Áp dụng định lí Pythagore để tính độ dài các cạnh của tam giác ABC .

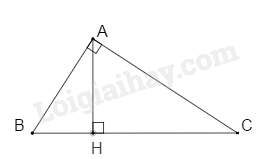
Áp dụng định lí Pythagore cho tam giác ABH vuông tại H, ta có:

$\begin{array}{l}A{B^2} = B{H^2} + A{H^2} \Rightarrow B{H^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\\ \Rightarrow BH = 3(cm)\end{array}$

Suy ra: $BC = HB + HC = 3 + \sqrt {184}$

Áp dụng định lí Pythagore cho tam giác AHC vuông tại H ta có:

$A{C^2} = C{H^2} + A{H^2} = {4^2} + {\left( {\sqrt {184} } \right)^2} = 200 \Rightarrow AC = \sqrt {200}$

Vậy chu vi tam giác ABC là: $AB + AC + BC = 5 + \sqrt {200} + 3 + \sqrt {184} \approx 35,7cm$