Cho \(\Delta ABC\) nhọn (AB < AC). Hai đường cao BE và CF.
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ và \(AE.AC = AF.AB\)
b) Trên tia BE lấy điểm N sao cho \(\widehat {ANC} = {90^0}\) (E nằm giữa B và N). Chứng minh $\Delta ANE\backsim \Delta ACN$ và \(A{N^2} = AE.AC\).
c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo \(\widehat {AMB}\).
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng suy ra \(AE.AC = AF.AB\).
b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{N^2} = NE.NB\).
c) Dựa vào các tỉ số của câu a và b suy ra \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$.
Từ đó suy ra số đo góc AMB.
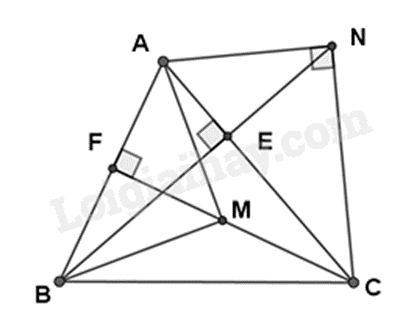
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^0}\)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABE\backsim \Delta ACF$ (g.g). (đpcm)
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\) hay \(AB.AF = AE.AC\)(đpcm) (1)
b) Xét \(\Delta ANE\) và \(\Delta ACN\) có:
\(\widehat {AEN} = \widehat {ANC} = {90^0}\)
\(\widehat {NAC}\) chung
Suy ra $\Delta ANE\backsim \Delta ACN$ (g.g).
Suy ra \(\frac{{AN}}{{AC}} = \frac{{AE}}{{AN}}\) hay \(A{N^2} = AC.AE\) (đpcm). (2)
c) Từ (1) và (2) suy ra \(AB.AF = A{N^2}\).
Mà AM = AN (gt) suy ra \(AM = AB.AF\) hay \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\).
Xét \(\Delta AMF\) và \(\Delta ABM\) có:
\(\widehat {BAM}\) chung
\(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) (cmt)
Suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$
Suy ra \(\widehat {AMB} = \widehat {AFM} = {90^0}\).