Cho tam giác ABC nhọn có AB — Không quảng cáo

Đề bài

Cho $\Delta ABC$ nhọn có AB < AC. Đường cao AH. Qua H vẽ $HM \bot AB$ và $HN \bot AC$ .

a) Chứng minh $\Delta AMH\backsim \Delta AHB$ .

b) Chứng minh $AN.AC = A{H^2}$ .

c) Vẽ đường cao BD cắt AH tại E. Qua D vẽ đường thẳng song song với MN cắt AB tại F. Chứng minh $\widehat {AEF} = \widehat {ABC}$ .

Phương pháp giải

a) Chứng minh $\Delta AMH\backsim \Delta AHB\left( g.g \right)$

b) Chứng minh $\Delta ANH\backsim \Delta AHC\left( g.g \right)$ suy ra $\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}$ suy ra $AN.AC = A{H^2}$ .

c) Áp dụng định lý Thales để chứng minh $\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\left( { = \frac{{AD}}{{AN}}} \right)$

Chứng minh $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ suy ra $\widehat {AEF} = \widehat {AHM}$ mà $\widehat {AHM} = \widehat {ABC}$ nên $\widehat {AEF} = \widehat {ABC}$ .

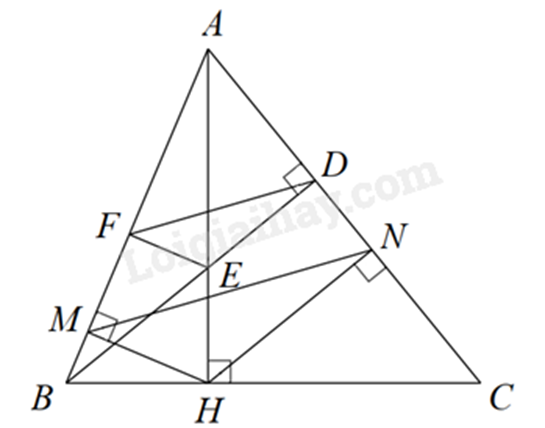
a) Xét $\Delta AMH$ và $\Delta AHB$ có:

$\widehat {AMH} = \widehat {AHB}\left( { = {{90}^0}} \right)$

$\widehat A$ chung

suy ra $\Delta AMH\backsim \Delta AHB\left( g.g \right)$ (đpcm)

b) Xét $\Delta ANH$ và $\Delta AHC$ có:

$\widehat {ANH} = \widehat {AHC}\left( { = {{90}^0}} \right)$

$\widehat A$ chung

suy ra $\Delta ANH\backsim \Delta AHC\left( g.g \right)$

suy ra $\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}$ suy ra $AN.AC = A{H^2}$ (đpcm)

c) Vì DF // NM nên $\frac{{AF}}{{AM}} = \frac{{AD}}{{AN}}$

Vì DE // HN nên $\frac{{AE}}{{AH}} = \frac{{AD}}{{AN}}$

suy ra $\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}$

Xét $\Delta AFE$ và $\Delta AMH$ có:

$\widehat A$ chung

$\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}$

suy ra $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ nên $\widehat {AEF} = \widehat {AHM}$

Mà $\widehat {AHM} = \widehat {ABC}$ (vì $\Delta AMH\backsim \Delta AHB$ )

Do đó $\widehat {AEF} = \widehat {ABC}$ (đpcm)