Cho tam giác ABC nhọn, hai đường cao BD và CE. Trên tia đối — Không quảng cáo

Phương pháp giải

Áp dụng tính chất trong tam giác vuông 2 góc nhọn phụ nhau, tính chất 2 góc kề bù, dấu hiệu nhận biết tam giác vuông cân.

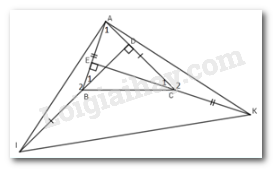
Xét ${\Delta}ABD$ có: $\widehat {{A_1}} + \widehat {{B_1}} = {90^0}$ (trong tam giác vuông 2 góc nhọn phụ nhau)

Xét ${\Delta}AEC$ có: $\widehat {{A_1}} + \widehat {{C_1}} = {90^0}$ (trong tam giác vuông 2 góc nhọn phụ nhau)

$\Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)$.

Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)

Từ $\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}$ .

Xét $\Delta ABI$ và $\Delta KCA$ có:

$AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)$

$\Rightarrow \Delta ABI = \Delta KCA ({c - g - c})$$\Rightarrow AI = AK$ (2 cạnh tương ứng)

Phương pháp giải

Áp dụng tính chất trong tam giác vuông 2 góc nhọn phụ nhau, tính chất 2 góc kề bù, dấu hiệu nhận biết tam giác vuông cân.

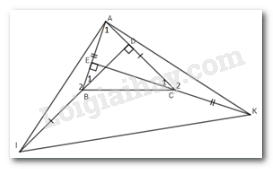
Ta có $AI = AK\left( {cmt} \right) \Rightarrow \Delta AIK$ cân tại A (*).

$\Delta ABI = \Delta KCA\left( {cmt} \right) \Rightarrow \widehat {AIB} = \widehat {CAK}(3)$(2 góc tương ứng)

Xét ${\Delta}AID$ có: $\widehat {AID} + \widehat {IAD} = {90^0}\left( 4 \right)$(trong tam giác vuông 2 góc nhọn phụ nhau)

Từ (3) và (4)$\Rightarrow \widehat {IAD} + \widehat {CAK} = {90^0} \Rightarrow \Delta AIK$ vuông tại A (**)

Từ (*) và (**) $\Rightarrow \Delta AIK$vuông cân tại $A.$