Đề bài
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
-
A.
\(20^\circ \)
-
B.
\(30^\circ \)
-
C.
\(40^\circ \)
-
D.
\(50^\circ \)
Phương pháp giải
+ Sử dụng tính chất đường trung trực
+ Sử dụng tính chất tam giác cân để tính góc \(EAF.\)
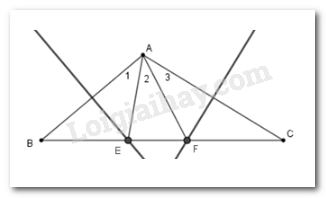
Vì E nằm trên đường trung trực của AB nên \(EA = EB\) ( tính chất) nên \(\widehat {{A_1}} = \widehat B\)
Vì F nằm trên đường trung trực của AC nên \(FA = FC\) ( tính chất) nên \(\widehat {{A_3}} = \widehat C\).
Do đó \(\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C = 180^\circ - 100^\circ = 80^\circ \)
\(\Rightarrow \widehat {{A_2}} = 100^\circ - 80^\circ = 20^\circ .\)
Đáp án : A