Cho tam giác ABC. Từ A vẽ một cung tròn có bán kính bằng BC — Không quảng cáo

Phương pháp giải

+) Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau,

+) Sử dụng hai góc bằng nhau ở vị trí so le trong ta chứng minh được hai đường thẳng song song

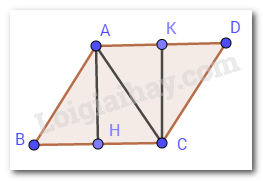
Xét $\Delta ABC$ và $\Delta CDA$ có:

$\begin{array}{l}AC\;\;chung\\AB = CD\;(cmt)\\BC = DA\;(cmt)\\ \Rightarrow \Delta ABC = \Delta CDA(c - c - c)\end{array}$

$\Rightarrow \widehat {ACB} = \widehat {CAD}$ (hai góc tương ứng)

Mà 2 góc này ở vị trí so le trong nên AD // BC.

Ta có: $\widehat {ACB} = \widehat {CAD}\;\;(cmt) \Rightarrow \widehat {ACH} = \widehat {CAK}$

Xét $\Delta AHC$ và $\Delta CKA$ có:

$\begin{array}{l}AC\;chung\\\widehat H = \widehat K = 90^\circ \;(gt)\\\widehat {ACH} = \widehat {CAK}\;\;\left( {cmt} \right)\end{array}$

$\Rightarrow \Delta AHC = \Delta CKA$ (cạnh huyền - góc nhọn)

$\Rightarrow AH = CK$ ( hai cạnh tương ứng).

Do đó, A,B,D là các khẳng định đúng