Đề bài
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
-
A.
Hình thang
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Phương pháp giải
Chứng minh tứ giác BHCD có BH // CD và HC // BD nên BHCD là hình bình hành.
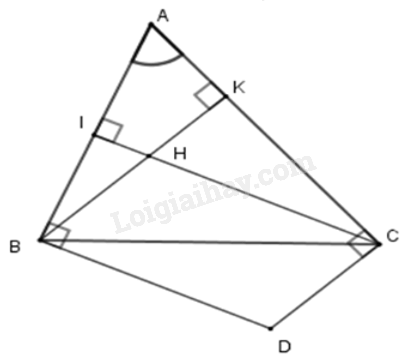
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành
Đáp án : B