Cho tam giác \({\rm{ABC}}\) với \(AB = 6{\rm{\;cm}},AC = 9{\rm{\;cm}}\).
a) Lấy các điểm \({\rm{M}},{\rm{N}}\) lần lượt trên các cạnh \({\rm{AB}},{\rm{AC}}\) sao cho \(AM = 4{\rm{\;cm}},AN = 6{\rm{\;cm}}\). Chứng minh rằng $\Delta AMN\backsim \Delta ABC$ và tìm tỉ số đồng dạng.
b) Lấy điểm \(P\) trên cạnh \({\rm{AC}}\) sao cho \(AP = 4{\rm{\;cm}}\). Chứng minh rằng $\Delta APB\backsim \Delta ABC$.
a) Áp dụng định lí Thales đảo chứng minh \({\rm{MN}}/\) /BC
Áp dụng định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
b) Chứng minh \(\Delta APB = \Delta AMN\left( {c - g - c} \right)\). Suy ra đpcm.
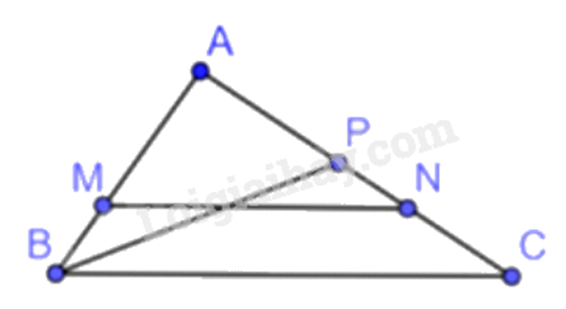
a) Xét \(\Delta {\rm{ABC}}\) có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\left( {\frac{4}{6} = \frac{6}{9} = \frac{2}{3}} \right)\)
nên MN//BC (định lí Thales đảo)
Suy ra $\Delta AMN\backsim \Delta ABC$ (định lí) với tỉ số đồng dạng \(\frac{2}{3}\)
b) Xét \(\Delta APB\) và \(\Delta AMN\) có: \(AP = AM\left( { = 4{\rm{\;cm}}} \right),\widehat A\) chung, \(AB = AN\left( { = 6{\rm{\;cm}}} \right)\) Suy ra \(\Delta APB = \Delta AMN\left( {c - g - c} \right)\left( 2 \right)\)
Từ (1) và (2) suy ra $\Delta APB\backsim \Delta ABC$