Cho tam giác ABC với đường trung tuyến AM và phân giác — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

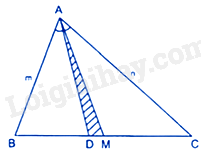
Vì tam giác ADM và tam giác ABC có chung chiều cao kẻ từ A đến BC nên \(\frac{{{S_{ADM}}}}{{{S_{ABC}}}} = \frac{{DM}}{{BC}} \Rightarrow {S_{ADM}} = \frac{{DM}}{{BC}}.{S_{ABC}}\)

Xét tam giác ABC có AD là đường phân giác của góc BAC nên: \(\frac{{DB}}{{DC}} = \frac{{BA}}{{CA}} = \frac{m}{n} \Rightarrow DB = mt,DC = nt\) (với \(t > 0\) )

Do đó, \(BC = DC + BD = \left( {m + n} \right)t\) , suy ra \(BM = \frac{1}{2}BC = \frac{{\left( {m + n} \right)t}}{2}\)

Ta có: \(DM = BM - DB = \frac{{\left( {m + n} \right)t - 2mt}}{2} = \frac{{\left( {n - m} \right)t}}{2}\)

Suy ra: \(\frac{{DM}}{{BC}} = \frac{{\frac{{\left( {n - m} \right)t}}{2}}}{{\left( {m + n} \right)t}} = \frac{{n - m}}{{2\left( {m + n} \right)}}\)

Vậy \({S_{AMD}} = \frac{{n - m}}{{2\left( {m + n} \right)}}S{  _{ABC}}\)