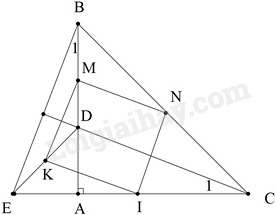
Cho tam giác ABC vuông cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AD. Gọi M, N, I, K theo thứ tự là các điểm thuộc các cạnh BD, BC, EC, ED sao cho
\(MN//CD,MN = \frac{1}{2}CD;KI//CD,KI = \frac{1}{2}CD;NI//BE,NI = \frac{1}{2}BE;MK//BE,MK = \frac{1}{2}BE\).Tứ giác MNIK là hình gì?
-
A.
Hình bình hành.
-
B.
Hình chữ nhật.
-
C.
Hình vuông.
-
D.
Hình thoi.
Do đó tứ giác MNIK là hình vuông.
Ta có: \(\Delta ACD = \Delta ABE(c.g.c)\)
Suy ra: CD = BE
Lại có: \(\widehat {{C_1}} = \widehat {{B_1}}\)
Mặt khác: \(\widehat {{B_1}}\) phụ với \(\widehat {BEC}\) nên \(\widehat {{C_1}}\) phụ với \(\widehat {BEC}\)
Do đó: \(CD \bot BE\)
Theo đề bài ta có:
\(\begin{array}{l}MN//CD,MN = \frac{1}{2}CD\\KI//CD,KI = \frac{1}{2}CD\\NI//BE,NI = \frac{1}{2}BE\\MK//BE,MK = \frac{1}{2}BE\end{array}\)
Từ đó suy ra MN = NI = KI = MK và \(MN \bot MK\)
Do đó tứ giác MNIK là hình vuông.
Đáp án : C