Cho tam giác \(ABC\) vuông có cạnh huyền \(AB = \sqrt {117} \;\;{\rm{cm,}}\,\,BC = 6\;\;{\rm{cm}}.\) Gọi \(K\) là trung điểm của đoạn thẳng \(AC\). Độ dài \(BK\) là
-
A.
\(3\;\;{\rm{cm}}\).
-
B.
\(4,5\;\;{\rm{cm}}\).
-
C.
\(7,5\;\;{\rm{cm}}\).
-
D.
\(10\;\;{\rm{cm}}\).
Áp dụng định lí Pythagore vào tam giác ABC để tính AC.
Tính độ dài CK.
Áp dụng định lí Pythagore vào tam giác BCK để tính BK.
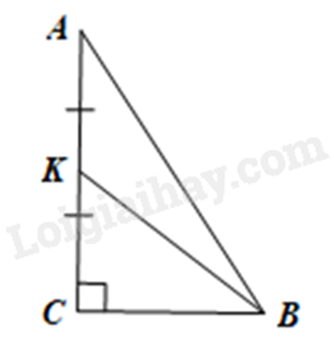
Xét \(\Delta ABC\) vuông tại \(C\), theo định lí Pythagore ta có:
\(A{C^2} = A{B^2} - B{C^2} = {\left( {\sqrt {117} } \right)^2} - {6^2} = 81\)
Suy ra \(AC = \sqrt {81} = 9\;\;{\rm{cm}}\)
Do \(K\) là trung điểm của đoạn thẳng \(AC\) nên \(CK = \frac{1}{2}AC = 4,5\;\;{\rm{cm}}\)
Xét \(\Delta BCK\) vuông tại \(C\), theo định lí Pythagore ta có:
\(B{K^2} = B{C^2} + C{K^2} = {6^2} + 4,{5^2} = 56,25\)
Suy ra \(BK = \sqrt {56,25} = 7,5\;\;{\rm{cm}}\).
Đáp án C.
Đáp án : C