Cho tam giác ABC vuông tại A AB — Không quảng cáo

Phương pháp giải

a) $\Delta ABH\backsim \Delta CBA$ (g.g) suy ra tỉ số các cạnh tương ứng của hai tam giác.

b) Chứng minh $AB.AE = AC.AF = A{H^2}$ thông qua chứng minh $\Delta AHE\backsim \Delta ABH$, $\Delta AHF\backsim \Delta ACH$.

c) Dựa vào b ta có tỉ số bằng nhau. Chứng minh $\Delta AEF\backsim \Delta ACB$ (c.g.c)

d) Chứng minh $\Delta HNI\backsim \Delta HFC\Rightarrow \frac{HN}{HI}=\frac{HF}{HC}$ suy ra $\Delta HFN\backsim \Delta HCI$.

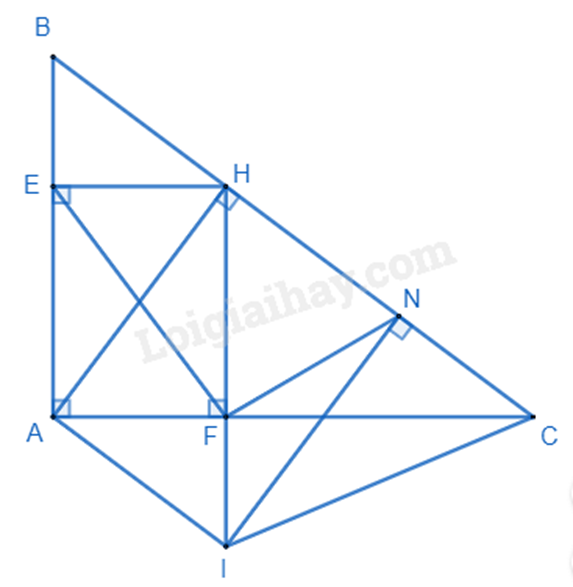
a) Xét $\Delta ABH$ và $\Delta CBA$ có:

$\widehat B$ chung

$\widehat H = \widehat A = \left( {{{90}^0}} \right)$

$\Rightarrow \Delta ABH\backsim \Delta CBA\left( g.g \right)$ (đpcm)

$\Rightarrow \frac{{AB}}{{BH}} = \frac{{BC}}{{AB}} \Rightarrow A{B^2} = BH.BC$ (đpcm)

b) Xét $\Delta AHE$ và $\Delta ABH$ có:

$\widehat A$ chung

$\widehat E = \widehat H\left( { = {{90}^0}} \right)$

$\Rightarrow \Delta AHE\backsim \Delta ABH\left( g.g \right)$

$\Rightarrow \frac{{AE}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow AE.AB = A{H^2}$ (1)

Xét $\Delta AHF$ và $\Delta ACH$ có:

$\widehat A$ chung

$\widehat F = \widehat H\left( { = {{90}^0}} \right)$

$\Delta AHF\backsim \Delta ACH\left( g.g \right)$

$\Rightarrow \frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF.AC = A{H^2}$ (2)

Từ (1) và (2) suy ra AE.AB = AF.AC (đpcm)

c) Theo ý b, ta có $AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}$.

Xét $\Delta AEF$ và $\Delta ACB$ có:

$\widehat A$ chung

$\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}$ (cmt)

$\Rightarrow \Delta AEF\backsim \Delta ACB$ (c.g.c) (đpcm)

d) Xét $\Delta HNI$ và $\Delta HFC$ có:

$\widehat H$ chung

$\widehat N = \widehat F = \left( {{{90}^0}} \right)$

$\Rightarrow \Delta HNI\backsim \Delta HFC\left( g.g \right)$

$\Rightarrow \frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}$

Xét $\Delta HFN$ và $\Delta HCI$ có:

$\widehat H$ chung

$\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}$ (cmt)

$\Rightarrow \Delta HFN\backsim \Delta HCI\left( c.g.c \right)$ (đpcm)