Cho tam giác ABC vuông tại A AB > AC, đường cao AH. Từ B kẻ — Không quảng cáo

Phương pháp giải

a) Chứng minh tứ giác ABKC có hai cạnh đối song song nên là hình thang và có một góc vuông nên là hình thang vuông.

b) Chứng minh $\Delta ABK\backsim \Delta CHA\left( g.g \right)$ suy ra tỉ số giữa các cạnh trong hai tam giác để chứng minh $AB.AC=AK.CH$.

c) Chứng minh $\Delta AHB\backsim \Delta CHA\left( g.g \right)$ để chứng minh $A{{H}^{2}}=HB.HC$.

d) Áp dụng $A{{H}^{2}}=HB.HC$ để tính AH, định lí Pythagore để tính AB.

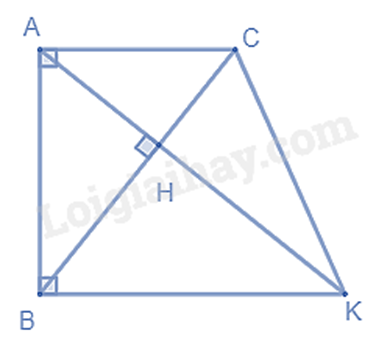
a) Ta có: \(AC \bot AB\left( {gt} \right),BK \bot AB\left( {gt} \right)\) \( \Rightarrow AC//BK\) nên tứ giác ABKC là hình thang.

Mà \(\widehat A = \widehat B = {90^0}\) nên ABKC là hình thang vuông.

b) Vì AC // BK nên \(\widehat {CAH} = \widehat {AKB}\) (hai góc so le trong)

Xét \(\Delta ABK\) và \(\Delta CHA\) có:

\(\widehat B = \widehat H\left( { = {{90}^0}} \right)\)

\(\widehat {CAH} = \widehat {AKB}\) (cmt)

$\Rightarrow \Delta ABK\backsim \Delta CHA\left( g.g \right)$ (đpcm)

\( \Rightarrow \frac{{AB}}{{AK}} = \frac{{CH}}{{CA}} \Rightarrow AB.CA = AK.CH\) (đpcm)

c) Ta có:

\(\left. \begin{array}{l}\widehat {HAC} + \widehat {ACH} = {90^0}\\\widehat {ABC} + \widehat {ACH} = {90^0}\end{array} \right\} \Rightarrow \widehat {HAC} = \widehat {ABC}\)

Xét \(\Delta AHB\) và \(\Delta CHA\) có:

\(\widehat {AHB} = \widehat {CHA}\left( { = {{90}^0}} \right)\)

\(\widehat {HAC} = \widehat {ABC}\)

$\Rightarrow \Delta AHB\backsim \Delta CHA\left( g.g \right)$

\( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Rightarrow A{H^2} = BH.CH\) (đpcm)

d) Ta có: \(A{H^2} = BH.CH = 9.16 = 144 = {12^2}\)

\( \Rightarrow AH = 12\left( {cm} \right)\)

Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có:

\(\begin{array}{l}A{B^2} = A{H^2} + H{B^2} = {12^2} + {9^2} = 225\\ \Rightarrow AB = 15\left( {cm} \right)\end{array}\)

Vậy AH = 12cm, AB = 15cm.