Cho tam giác ABC vuông tại A AB > AC. Gọi I là trung điểm

Đề bài

Cho tam giác ABC vuông tại A (AB > AC). Gọi I là trung điểm của AB. Kẻ IN vuông góc với BC tại N (N thuộc BC).

a) Chứng minh $\Delta ACB\backsim \Delta NIB$. Từ đó suy ra $BA.BI = BC.BN$.

b) Giả sử AC = 6cm, BC = 10cm. Tính BN.

c) Chứng minh $\widehat {IAN} = \widehat {ICN}$.

d) Chứng minh $A{C^2} = N{C^2} - N{B^2}$.

Phương pháp giải

a) Chứng minh $\Delta ACB\backsim \Delta NIB$ (g.g) suy ra tỉ số bằng nhau của các cặp cạnh tương ứng.

b) Dựa vào định lí Pythagore để tính AB. Sử dụng tỉ số bằng nhau của phần a để tính BN.

c) Chứng minh $\Delta ABN\backsim \Delta CBI$ (c.g.c) để chứng minh $\widehat {IAN} = \widehat {ICN}$.

d) Kẻ $AH \bot BC$ tại H. Chứng minh $A{C^2} = CH.CB$.

Chứng minh BN = NH.

Sử dụng hằng đẳng thức hiệu hai bình phương để chứng minh $A{C^2} = CH.CB = N{C^2} - N{B^2}$.

Chú ý: Độ dài các cạnh chỉ sử dụng cho ý b nên không được tính độ dài cạnh để chứng minh.

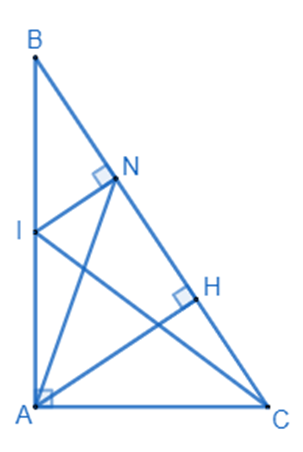
a) Xét $\Delta ACB$ và $\Delta NIB$ có:

$\widehat B$ chung

$\widehat A = \widehat N\left( { = {{90}^0}} \right)$

$\Rightarrow \Delta ACB\backsim \Delta NIB\left( g.g \right)$ (đpcm)

$ \Rightarrow \frac{{BA}}{{BN}} = \frac{{BC}}{{BI}}$

$ \Rightarrow BA.BI = BC.BN$ (đpcm)

b) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

$\begin{array}{l}A{B^2} = B{C^2} - A{C^2} = {10^2} - {6^2} = 64\\ \Rightarrow AB = 8\left( {cm} \right)\end{array}$

I là trung điểm của AB nên AI = IB = $\frac{1}{2}$AB = 4cm

Ta có: $BA.BI = BC.BN$

$\begin{array}{l}8.4 = 10.BN\\ \Rightarrow BN = \frac{{8.4}}{{10}} = 3,2\left( {cm} \right)\end{array}$

c) Xét $\Delta ABN$ và $\Delta CBI$ có:

$\frac{{BA}}{{BN}} = \frac{{BC}}{{BI}}\left( {cmt} \right)$

$\widehat B$ chung

$\Rightarrow \Delta ABN\backsim \Delta CBI\left( c.g.c \right)$

$ \Rightarrow \widehat {IAN} = \widehat {ICN}$ (đpcm)

d) Kẻ $AH \bot BC$ tại H.

Xét $\Delta AHC$ và $\Delta BAC$ có:

$\widehat A = \widehat H\left( { = {{90}^0}} \right)$

$\widehat C$ chung

$\Rightarrow \Delta AHC\backsim \Delta BAC\left( g.g \right)$

$ \Rightarrow \frac{{AC}}{{CH}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = CH.BC$.

Vì $IN \bot BC;AH \bot BC \Rightarrow IN//AH$

Xét tam giác ABH có IN // AH, I là trung điểm của AB nên IN là đường trung bình của tam giác ABH.

$ \Rightarrow $ N là trung điểm của BH $ \Rightarrow BN = NH$.

Ta có: $CH.CB$$ = \left( {CN - NH} \right)\left( {CN + BN} \right)$$ = \left( {CN - BN} \right)\left( {CN + BN} \right)$$ = C{N^2} - B{N^2}$

$ \Rightarrow A{C^2} = C{N^2} - B{N^2}$ (đpcm)